Míg vannak, akik nagyképernyős LCD televízióra, vagy új autóra áhítoznak, mivel ajándékozhatja meg magát az, akinek már-már mindene megvan? Egy telekkel? Nade hol legyen, mi a legmenőbb hely - azért ne ott legyen már, ahol bárkinek lehet. Talán a Holdon? Ma már semmi sem lehetetlen, sőt, már egy ideje nem az. Az ember azt hinné, hogy vicc az egész. Hogyan is lehetne áruba bocsátani a csillagokat, az emberiség közös "tulajdonát"? Pedig lehet, mégpedig törvényes keretek között. Mégis hogyan lehetséges ez?  Úgy, hogy az 1967-es Nemzetközi Űregyezmény csak a különböző országoknak tiltotta meg, hogy bármiféle jogot formáljanak a Holdra, ám magánembereknek nem. Ráadásul az amerikai törvénykezés alapján, aki egy telekkönyvbe beíratja magát egy gazdátlan földterület tulajdonosaként, és nyolc éven át senki sem emel ez ellen kifogást, az a föld tényleges tulajdonosa lesz. Felfigyelt erre Dennis Hope Nevadában élő cipőárus, aki még 1980-ban bejegyeztette magát Hold tulajdonosként - jobb híján - a San Francisco-i telekkönyvbe. Ezt követően arra is volt gondja, hogy cselekedetéről informálja az Egyesült Államok és a Szovjetunió kormányait, majd az ENSZ-et is. És mivel sehonnan sem érkezett elutasítás, fellebbezés vagy tiltakozás, a Hold kizárólagos tulajdonosává váló úriember az internet segítségével elkezdte árusítani a Holdat, mára már világméretű, ügynöki hálózattal működő, Hold Nagykövetség (Lunar Embassy) keretein belül. Egy holdnyi Hold ára 7800 Ft, amiért minden telektulajdonos kap a tulajdonáról egy tanúsítványt, megkapja a Hold alkotmányát, és egy térképet, amelyen be van jelölve, hol is van a telke.
Úgy, hogy az 1967-es Nemzetközi Űregyezmény csak a különböző országoknak tiltotta meg, hogy bármiféle jogot formáljanak a Holdra, ám magánembereknek nem. Ráadásul az amerikai törvénykezés alapján, aki egy telekkönyvbe beíratja magát egy gazdátlan földterület tulajdonosaként, és nyolc éven át senki sem emel ez ellen kifogást, az a föld tényleges tulajdonosa lesz. Felfigyelt erre Dennis Hope Nevadában élő cipőárus, aki még 1980-ban bejegyeztette magát Hold tulajdonosként - jobb híján - a San Francisco-i telekkönyvbe. Ezt követően arra is volt gondja, hogy cselekedetéről informálja az Egyesült Államok és a Szovjetunió kormányait, majd az ENSZ-et is. És mivel sehonnan sem érkezett elutasítás, fellebbezés vagy tiltakozás, a Hold kizárólagos tulajdonosává váló úriember az internet segítségével elkezdte árusítani a Holdat, mára már világméretű, ügynöki hálózattal működő, Hold Nagykövetség (Lunar Embassy) keretein belül. Egy holdnyi Hold ára 7800 Ft, amiért minden telektulajdonos kap a tulajdonáról egy tanúsítványt, megkapja a Hold alkotmányát, és egy térképet, amelyen be van jelölve, hol is van a telke.
A cég Magyarországon is megjelent, és ma már akinek úgy tetszik, nevet adhat egy csillagnak. Cserébe kap egy tanúsítványt a választott csillag koordinátáival, merített papíron, olasz képkeretben, díszszalaggal átkötve, az ISR (International Star Registry - Nemzetközi Csillagregisztráció) arany pecsétjével ellátva.
Azt gondolnánk, hogy ennyi idő után mára már a Naprendszer szinte minden csillaga, illetve a Holdon minden "talpalatnyi hely" elkelt. De nem! Ékes bizonyíték erre, hogy a napokban Angeles Duran spanyol hölgy lett a boldog tulajdonosa a Földtől 149 millió kilométer átlagos távolságra lévő G2 színképosztályba tartozó csillagnak - a Napnak.
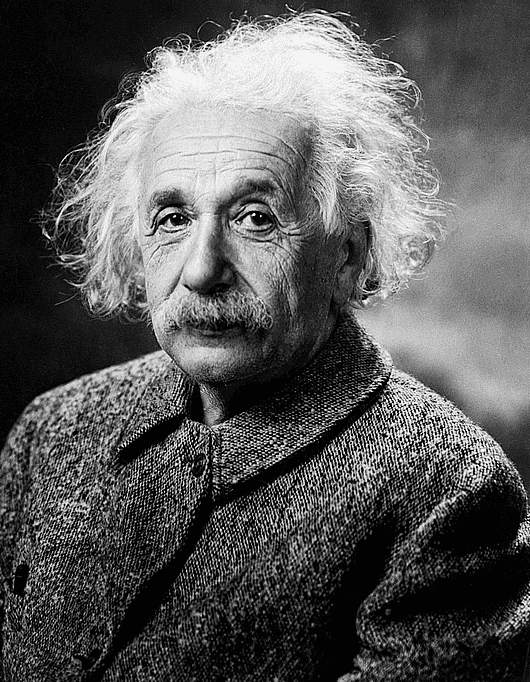 vagy méginkább a fotoelektromos jelenség. 1921-ben fizikai Nobel-díjjal jutalmazták utóbbiért, ami elhomályosíthatja a róla elnevezett elmélet jelentőségét - de utánagondolva beláthatjuk, hogy akkoriban a kísérleti alátámasztása még nem volt megvalósítható oly mértékben mint ma, emiatt emelték ki az odaítélés okaként a fotoelektromos jelenséget.
vagy méginkább a fotoelektromos jelenség. 1921-ben fizikai Nobel-díjjal jutalmazták utóbbiért, ami elhomályosíthatja a róla elnevezett elmélet jelentőségét - de utánagondolva beláthatjuk, hogy akkoriban a kísérleti alátámasztása még nem volt megvalósítható oly mértékben mint ma, emiatt emelték ki az odaítélés okaként a fotoelektromos jelenséget.  -szorosa lesz. /Konkrét pédát adva: egy 100 cm hosszú rudat egy, a fénysebesség felével haladó megfigyelő 86,6 cm-nek érzékel./
-szorosa lesz. /Konkrét pédát adva: egy 100 cm hosszú rudat egy, a fénysebesség felével haladó megfigyelő 86,6 cm-nek érzékel./
 szerint a tömeg és az energia (pontosabban az energia-impulzus tenzor) „meggörbíti” a téridőt, és a görbület hatással van a szabad részecskék mozgására, sőt még a fényére is. Az elmélet felhasználható a Világegyetem fejlődésével kapcsolatos modellek felállítására, és így a kozmológia alapvető eszköze. Ez az elmélet jelenti az alapját a kozmológia standard modelljének, és ez ad eszközt ahhoz, hogy megértsük a Világegyetem tulajdonságait, azokat a tulajdonságokat, amelyeket csak jóval Einstein halála után fedeztek fel.
szerint a tömeg és az energia (pontosabban az energia-impulzus tenzor) „meggörbíti” a téridőt, és a görbület hatással van a szabad részecskék mozgására, sőt még a fényére is. Az elmélet felhasználható a Világegyetem fejlődésével kapcsolatos modellek felállítására, és így a kozmológia alapvető eszköze. Ez az elmélet jelenti az alapját a kozmológia standard modelljének, és ez ad eszközt ahhoz, hogy megértsük a Világegyetem tulajdonságait, azokat a tulajdonságokat, amelyeket csak jóval Einstein halála után fedeztek fel. Nevezik kormányozható léghajónak is, megkülönböztetve a nem kormányozható léggömbtől. Szükség volt olyan légi járműre, amely nem csak a szelek kénye kedvére halad a levegőben. A jobb légellenállás miatt a szivar alakú ballonokat kezdték alkalmazni - ettől kezdve már a léggömb helyett a léghajó elnevezést használták. A léghajóban a kis sűrűséget valamilyen töltőgáz biztosítja. Ez kezdetben a hidrogén volt, de mivel a hidrogén robbanásveszélyes, áttértek a nála kétszer nagyobb sűrűségű hélium töltőgázra. A hélium kémiai semlegessége, és kis sűrűsége miatt jobban megfelel a léghajók számára. Szerkezetileg háromféle típusa terjedt el: merev falú, félmerev, nem merev. Legkedvezőbb légellenállása a merev falú léghajónak van. A léghajó előrehaladását általában motor által hajtott légcsavar biztosítja. A magassági kormányzást részben a kormányberendezés, illetve elmozdítható súlyok biztosítják. A nagy szerkezeti méretek miatt gyors közlekedésre nem alkalmas. (Bár csúcssebessége megközelítette a 120 km/h-t.) Hátránya, hogy a le- és felszálláshoz többnyire különleges kikötésre van szükség. Az időjárás viszontagságait is nehezen bírja. Előnye viszont, hogy a levegőben maradáshoz csak minimális energiát igényel, csendes, motorja kevésbé környezetszennyező, mint egy repülőgépé, és nagy vagy kényes rakomány szállítására is alkalmas.
Nevezik kormányozható léghajónak is, megkülönböztetve a nem kormányozható léggömbtől. Szükség volt olyan légi járműre, amely nem csak a szelek kénye kedvére halad a levegőben. A jobb légellenállás miatt a szivar alakú ballonokat kezdték alkalmazni - ettől kezdve már a léggömb helyett a léghajó elnevezést használták. A léghajóban a kis sűrűséget valamilyen töltőgáz biztosítja. Ez kezdetben a hidrogén volt, de mivel a hidrogén robbanásveszélyes, áttértek a nála kétszer nagyobb sűrűségű hélium töltőgázra. A hélium kémiai semlegessége, és kis sűrűsége miatt jobban megfelel a léghajók számára. Szerkezetileg háromféle típusa terjedt el: merev falú, félmerev, nem merev. Legkedvezőbb légellenállása a merev falú léghajónak van. A léghajó előrehaladását általában motor által hajtott légcsavar biztosítja. A magassági kormányzást részben a kormányberendezés, illetve elmozdítható súlyok biztosítják. A nagy szerkezeti méretek miatt gyors közlekedésre nem alkalmas. (Bár csúcssebessége megközelítette a 120 km/h-t.) Hátránya, hogy a le- és felszálláshoz többnyire különleges kikötésre van szükség. Az időjárás viszontagságait is nehezen bírja. Előnye viszont, hogy a levegőben maradáshoz csak minimális energiát igényel, csendes, motorja kevésbé környezetszennyező, mint egy repülőgépé, és nagy vagy kényes rakomány szállítására is alkalmas. Úgy, hogy az 1967-es Nemzetközi Űregyezmény csak a különböző országoknak tiltotta meg, hogy bármiféle jogot formáljanak a Holdra, ám magánembereknek nem. Ráadásul az amerikai törvénykezés alapján, aki egy telekkönyvbe beíratja magát egy gazdátlan földterület tulajdonosaként, és nyolc éven át senki sem emel ez ellen kifogást, az a föld tényleges tulajdonosa lesz. Felfigyelt erre Dennis Hope Nevadában élő cipőárus, aki még 1980-ban bejegyeztette magát Hold tulajdonosként - jobb híján - a San Francisco-i telekkönyvbe. Ezt követően arra is volt gondja, hogy cselekedetéről informálja az Egyesült Államok és a Szovjetunió kormányait, majd az ENSZ-et is. És mivel sehonnan sem érkezett elutasítás, fellebbezés vagy tiltakozás, a Hold kizárólagos tulajdonosává váló úriember az internet segítségével elkezdte árusítani a Holdat, mára már világméretű, ügynöki hálózattal működő, Hold Nagykövetség (Lunar Embassy) keretein belül. Egy holdnyi Hold ára 7800 Ft, amiért minden telektulajdonos kap a tulajdonáról egy tanúsítványt, megkapja a Hold alkotmányát, és egy térképet, amelyen be van jelölve, hol is van a telke.
Úgy, hogy az 1967-es Nemzetközi Űregyezmény csak a különböző országoknak tiltotta meg, hogy bármiféle jogot formáljanak a Holdra, ám magánembereknek nem. Ráadásul az amerikai törvénykezés alapján, aki egy telekkönyvbe beíratja magát egy gazdátlan földterület tulajdonosaként, és nyolc éven át senki sem emel ez ellen kifogást, az a föld tényleges tulajdonosa lesz. Felfigyelt erre Dennis Hope Nevadában élő cipőárus, aki még 1980-ban bejegyeztette magát Hold tulajdonosként - jobb híján - a San Francisco-i telekkönyvbe. Ezt követően arra is volt gondja, hogy cselekedetéről informálja az Egyesült Államok és a Szovjetunió kormányait, majd az ENSZ-et is. És mivel sehonnan sem érkezett elutasítás, fellebbezés vagy tiltakozás, a Hold kizárólagos tulajdonosává váló úriember az internet segítségével elkezdte árusítani a Holdat, mára már világméretű, ügynöki hálózattal működő, Hold Nagykövetség (Lunar Embassy) keretein belül. Egy holdnyi Hold ára 7800 Ft, amiért minden telektulajdonos kap a tulajdonáról egy tanúsítványt, megkapja a Hold alkotmányát, és egy térképet, amelyen be van jelölve, hol is van a telke.  A véletlenül kiömlött nitroglicerint az ott lévő kovaföld fölitta, és Nobel rájött, hogy az így képződő, jól kezelhető anyag, ütésre nem érzékeny, tehát biztonságosan szállítható, de gyutaccsal ugyanúgy robban, mint a nitroglicerin - tehát feltalálja a dinamitot.
A véletlenül kiömlött nitroglicerint az ott lévő kovaföld fölitta, és Nobel rájött, hogy az így képződő, jól kezelhető anyag, ütésre nem érzékeny, tehát biztonságosan szállítható, de gyutaccsal ugyanúgy robban, mint a nitroglicerin - tehát feltalálja a dinamitot. 

 Bizonyára nagyon meglepődött az első ember, aki méregetés közben észrevette, hogy bármekkora kört is mérjünk le, a kerület mindig kb. háromszorosa az átmérőnek. (Ennél meglepőbb már csak az lehetne, ha ez az arány pontosan 3 volna.) A π egy természeti állandó, amely a bennünket körülvevő világ egyik fontos jellemzője. Feltenni a kérdést, hogy miért annyi a π amennyi, fel lehet ugyan, de a válaszra valószínűleg hiába várnánk.
Bizonyára nagyon meglepődött az első ember, aki méregetés közben észrevette, hogy bármekkora kört is mérjünk le, a kerület mindig kb. háromszorosa az átmérőnek. (Ennél meglepőbb már csak az lehetne, ha ez az arány pontosan 3 volna.) A π egy természeti állandó, amely a bennünket körülvevő világ egyik fontos jellemzője. Feltenni a kérdést, hogy miért annyi a π amennyi, fel lehet ugyan, de a válaszra valószínűleg hiába várnánk.

